🆀
for i in range(n): # n -2
for j in range(i+1, n): # n -1
O(1)의 작업
반복 횟수 계산 :
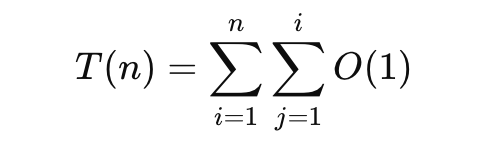

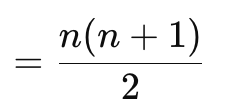
시간 복잡도 : O(n^2)
🆀
for i in range(n): # n -2:
for j in range(i+1, n): # n -1
for k in range(j+1, n): # n
O(1)의 작업
반복 횟수 계산 :
루프가 모든 가능한 (i, j, k) 조합을 순회할 때 루프의 전체 실행 횟수 = 그 조합의 개수
0 ≤ i < j < k < n 조건을 만족하는 모든 조합을 한번씩 순회하는 구조
so, 조합 식으로 계산 (nCr)
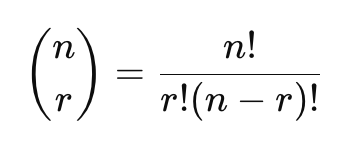

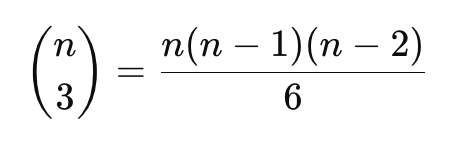
시간 복잡도 : O(n^3)
🆀
순열 : 중복 없이 순서만 다른 경우 (nPr)

for i in range(n):
for j in range(n):
for k in range(n):
if i != j and j != k and i != k:
O(1)의 작업
반복 횟수 계산 :
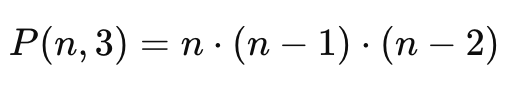
시간 복잡도 : O(n^3)
🆀
for i in range(n): # n
for j in range(n): # n
for k in range(n): # n
반복 횟수 : n^3
시간 복잡도 : O(n^3)
반응형
'기타 문제 풀이' 카테고리의 다른 글
| [백준] 1181 단어 정렬 (0) | 2025.05.18 |
|---|---|
| [백준] 11931 수 정렬하기 4 (0) | 2025.05.12 |
| [백준] 10171, 10172 고양이와 개 (4) | 2024.12.24 |
| [프로그래머스] Lv.1 실패율 (3) | 2024.11.22 |
| [백준] 2743 단어 길이 재기 (1) | 2024.11.22 |